一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶.设行驶的时间为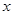 (时),两车之间的距离为
(时),两车之间的距离为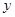 (千米),图中的折线表示从两车出发至快车到达乙地过程中
(千米),图中的折线表示从两车出发至快车到达乙地过程中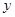 与
与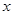 之间的函数关系.
之间的函数关系.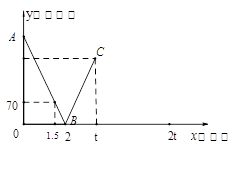
(1)根据图中信息,求线段AB所在直线的函数解析式和甲乙两地之间的距离;
(2)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(3)若快车到达乙地后立刻返回甲地,慢车到达甲地后停止行驶,请你在图中画出快车从乙地返回到甲地过程中
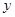 关于
关于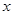 的函数的大致图象.
的函数的大致图象.
相关知识点
推荐套卷

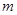 和
和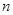 所表示的数分别为:
所表示的数分别为: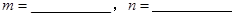 ;
;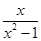 (
(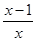 -2),其中
-2),其中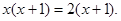
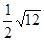 -(5-π)0+
-(5-π)0+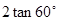
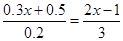 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。 ( )
( )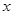 +5)=2(2
+5)=2(2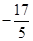 .
.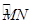 上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.
上一动点(B不与点M、N重合),∠MON=90°,BA⊥OM于点A,BC⊥ON于点C,点D、E、F、G分别是线段OA、AB、BC、CO的中点,GF与CE相交于点P,DE与AG相交于点Q.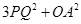 的值.
的值.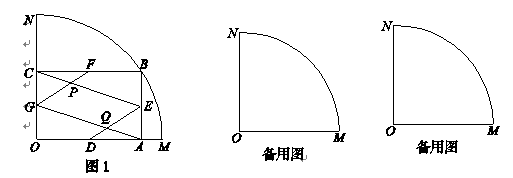
 经过点A(
经过点A( ,4),且与
,4),且与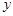 轴相交于点C. 点B在
轴相交于点C. 点B在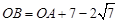 . △ABC的面积为S.
. △ABC的面积为S.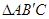 ,求点
,求点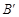 的坐标.
的坐标.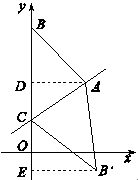
 粤公网安备 44130202000953号
粤公网安备 44130202000953号