(1)计算;|-1|-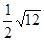 -(5-π)0+
-(5-π)0+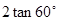
(2)依据下列解方程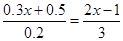 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
解:原方程可变形为 ( )
( )
去分母,得3(3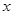 +5)=2(2
+5)=2(2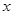 -1).
-1).
去括号,得9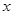 +15=4
+15=4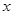 -2.
-2.
( ),得9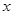 -4
-4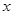 =-15-2. ( )
=-15-2. ( )
合并,得5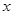 =-17.
=-17.
( ),得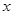 =
=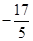 .
.
推荐套卷
(1)计算;|-1|-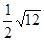 -(5-π)0+
-(5-π)0+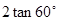
(2)依据下列解方程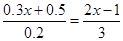 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据。
解:原方程可变形为 ( )
( )
去分母,得3(3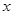 +5)=2(2
+5)=2(2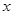 -1).
-1).
去括号,得9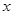 +15=4
+15=4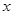 -2.
-2.
( ),得9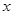 -4
-4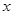 =-15-2. ( )
=-15-2. ( )
合并,得5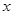 =-17.
=-17.
( ),得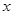 =
=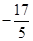 .
.