如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.
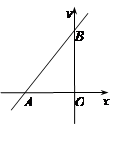
(1)求k的值;
(2)若P为直线AB上一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形,求点P的坐标;
(3)在(2)的条件下,连结PO,△PBO是等腰三角形吗?如果是,试说明理由,如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.
相关知识点
推荐套卷
如图,在直角坐标系中,已知直线y=kx+6与x轴、y轴分别交于A、B两点,且△ABO的面积为12.
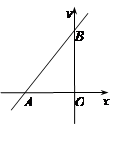
(1)求k的值;
(2)若P为直线AB上一动点,P点运动到什么位置时,△PAO是以OA为底的等腰三角形,求点P的坐标;
(3)在(2)的条件下,连结PO,△PBO是等腰三角形吗?如果是,试说明理由,如果不是,请在线段AB上求一点C,使得△CBO是等腰三角形.