学完“轴对称”这一章后,老师布置了一道思考题:如图所示,点M,N分别在等边△ABC的BC、CA边上,且BM=CN,AM,BN交于点Q,求证:∠BQM=60°.
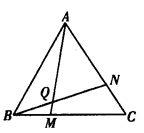
(1)请你完成这道思考题:
(2)做完(1)后,同学们在老师的启发下进行了反思,提出许多问题,如:
①若将题中“BM=CN”与“∠BQM=60°”的位置交换,得到的是否仍是真命题?
②若将题中的点M,N分别移动到BC,CA的延长线上,是否仍能得到∠BQM=60 ?
?
③若将题中的条件“点M,N分别在正三角形ABC的BC、CA边上”改为“点M,N分别在正方形ABCD的BC,CD边上”,是否仍能得到∠BQM=60°?……
请你作出判断,在下列横线上填写“是”或“否”:
①________;②_______;③________.并对②,③的判断,选择一个画出图形,并给出证明.