如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.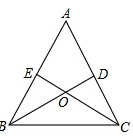
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
相关知识点
推荐套卷
如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC.
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.