（1）如图，在Rt△ABC中，∠C=90°，AC=BC，小明为了求tan67．5°值，他延长CB到D，使BD=BA，连接AD，请你根据图形计算tan67．5°；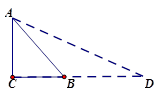
（2）请你仿照小明的方法构造图形求tan75°．
，其中
,n=-3．
．
）-2-（π-3．14）0+2-1+|
|
．相关知识点
推荐套卷
（1）如图，在Rt△ABC中，∠C=90°，AC=BC，小明为了求tan67．5°值，他延长CB到D，使BD=BA，连接AD，请你根据图形计算tan67．5°；
（2）请你仿照小明的方法构造图形求tan75°．
粤公网安备 44130202000953号