现有A,B两个投资项目,投资两项目所获得利润分别是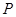 和
和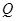 (万元),它们与投入资金
(万元),它们与投入资金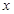 (万元)的关系依次是:其中
(万元)的关系依次是:其中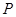 与
与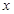 平方根成正比,且当
平方根成正比,且当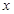 为4(万元)时
为4(万元)时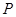 为1(万元),又
为1(万元),又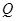 与
与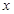 成正比,当
成正比,当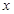 为4(万元)时
为4(万元)时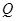 也是1(万元);某人甲有3万元资金投资.
也是1(万元);某人甲有3万元资金投资.
(Ⅰ)分别求出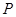 ,
,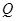 与
与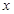 的函数关系式;
的函数关系式;
(Ⅱ)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?
推荐套卷
现有A,B两个投资项目,投资两项目所获得利润分别是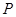 和
和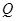 (万元),它们与投入资金
(万元),它们与投入资金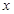 (万元)的关系依次是:其中
(万元)的关系依次是:其中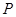 与
与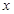 平方根成正比,且当
平方根成正比,且当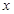 为4(万元)时
为4(万元)时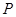 为1(万元),又
为1(万元),又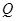 与
与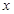 成正比,当
成正比,当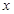 为4(万元)时
为4(万元)时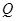 也是1(万元);某人甲有3万元资金投资.
也是1(万元);某人甲有3万元资金投资.
(Ⅰ)分别求出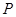 ,
,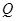 与
与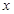 的函数关系式;
的函数关系式;
(Ⅱ)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?