某学校900名学生在一次百米测试中，成绩全部介于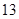
秒与
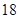秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组
，第二组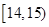
，…，第五组
，下图是按上述分组方法得到的频率分布直方图．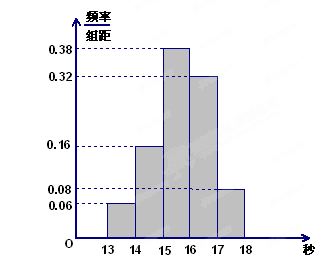
（1）若成绩小于14秒认为优秀，求该样本在这次百米测试中成绩优秀的人数；
（2）请估计学校900名学生中，成绩属于第四组的人数；
（3）请根据频率分布直方图，求样本数据的众数和中位数（保留两位小数）.
的最大值和最小值。
有最大值
，试求实数
的值。
使函数
是奇函数。
的函数
的最小值为
，试确定满足
的
的值，并对此时的
的最大值。
的奇偶性。相关知识点
推荐套卷
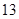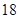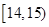某学校900名学生在一次百米测试中，成绩全部介于秒与秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组，第二组，…，第五组，下图是按上述分组方法得到的频率分布直方图．
（1）若成绩小于14秒认为优秀，求该样本在这次百米测试中成绩优秀的人数；
（2）请估计学校900名学生中，成绩属于第四组的人数；
（3）请根据频率分布直方图，求样本数据的众数和中位数（保留两位小数）.
粤公网安备 44130202000953号