如图，在平面直角坐标系中，OA=OB=OC=8，过点A的直线AD交BC于点D，交y轴与点G，△ABD的面积为△ABC面积的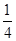
．
（1）求点D的坐标；
（2）过点C作CE⊥AD，交AB交于F，垂足为E．求证：OF=OG；
（3）若点F的坐标为（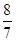
，0），在第一象限内是否存在点P，使△CFP是以CF为腰长的等腰直角三角形，若存在，请求出点P坐标；若不存在，请说明理由．
相关试题
，且点A、B到原点的距离相等，求x的值．
相关知识点
推荐套卷
如图，在平面直角坐标系中，OA=OB=OC=8，过点A的直线AD交BC于点D，交y轴与点G，△ABD的面积为△ABC面积的．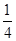
（1）求点D的坐标；
（2）过点C作CE⊥AD，交AB交于F，垂足为E．求证：OF=OG；
（3）若点F的坐标为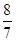（，0），在第一象限内是否存在点P，使△CFP是以CF为腰长的等腰直角三角形，若存在，请求出点P坐标；若不存在，请说明理由．
粤公网安备 44130202000953号