在如图所示的几何体中，四边形ABCD为矩形，平面ABEF
平面ABCD，EF//AB，
，AD=2，AB= AF=2EF=l，点P在棱DF上．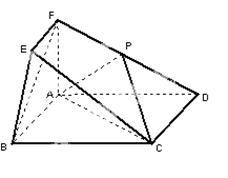
（1）若P为DF的中点，求证：BF//平面ACP
（2）若二面角D-AP-C的余弦值为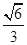
，求PF的长度．
相关试题
（
），其中
．
时，讨论函数
的单调性；
处有极值，求
的取值范围；
，不等式
在
上恒成立，求
的取值范围．
．
的解集是
，求实数
的值；
为整数，
，且函数
在
上恰有一个零点，求
.
的图像在
处的切线方程；
，求函数
在
上的最小值.
的值；
的值
，求实数m的值；
，求实数m的取值范围。相关知识点
推荐套卷
在如图所示的几何体中，四边形ABCD为矩形，平面ABEF平面ABCD，EF//AB，，AD=2，AB= AF=2EF=l，点P在棱DF上．
（1）若P为DF的中点，求证：BF//平面ACP
（2）若二面角D-AP-C的余弦值为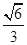，求PF的长度．
粤公网安备 44130202000953号