如图,地图上有一竖直放置的圆形标志物,圆心为C,与地面的接触点为G.与圆形标志物在同一平面内的地面上点P处有一个观测点,且PG=50m.在观测点正前方10m处(即PD=10m)有一个高位10m(即ED=10m)的广告牌遮住了视线,因此在观测点所能看到的圆形标志的最大部分即为图中从A到F的圆弧.
(1)若圆形标志物半径为25m,以PG所在直线为X轴,G为坐标原点,建立直角坐标系,求圆C和直线PF的方程;
(2)若在点P处观测该圆形标志的最大视角(即 )的正切值为
)的正切值为 ,求该圆形标志物的半径.
,求该圆形标志物的半径.
相关知识点
推荐套卷
 ,
, ,
, ,
, ,
, ,
, .
.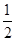 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 .
. ,
, ,
, .
. 时,求函数
时,求函数 的单调区间;
的单调区间; 上的最小值是
上的最小值是 ,求
,求 的值;
的值; 是函数
是函数 图象上任意不同的两点,线段
图象上任意不同的两点,线段 的中点为
的中点为 ,直线
,直线 ,证明:
,证明: .
. 的中心在原点,焦点在
的中心在原点,焦点在 轴上,离心率为
轴上,离心率为 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线 的焦点.
的焦点.
 与椭圆交于
与椭圆交于 两点,
两点, 点位于第一象限,
点位于第一象限, 是椭圆上位于直线
是椭圆上位于直线 的斜率为
的斜率为 ,求四边形
,求四边形 面积的最大值;
面积的最大值; ,问直线
,问直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号