已知椭圆C：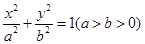
的离心率与双曲线
的离心率互为倒数，且以抛物线
的焦点F为右焦点．
（1）求椭圆C的标准方程；
（2）过右焦点F作斜率为
的直线l交曲线C于M、N两点，且
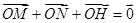，又点H关于原点O的对称点为点G，试问M、G、N、H四点是否共圆？若共圆，求出圆心坐标和半径；若不共圆，请说明理由．
相关试题
的前
项和
与通项
满足
，求
，
，
，
，若
，求实数
的值．
,求:
;(2)
;(3)函数
.
、
、
满足
，则称
比3接近0，求
、
，证明：
比
接近
；
的定义域
.任取
，
和
中接近0的那个值.写出函数推荐套卷
已知椭圆C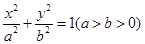：的离心率与双曲线的离心率互为倒数，且以抛物线的焦点F为右焦点．
（1）求椭圆C的标准方程；
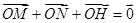（2）过右焦点F作斜率为的直线l交曲线C于M、N两点，且，又点H关于原点O的对称点为点G，试问M、G、N、H四点是否共圆？若共圆，求出圆心坐标和半径；若不共圆，请说明理由．
粤公网安备 44130202000953号