某产品按质量分为10个档次，生产第一档（即最低档次）的利润是每件8元，每提高一个档次，利润每件增加2元，但每提高一个档次，在相同的时间内，产量减少3件。如果在规定的时间内，最低档次的产品可生产60件。
（1）请写出相同时间内产品的总利润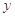
与档次
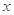之间的函数关系式，并写出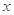的定义域．
（2）在同样的时间内，生产哪一档次产品的总利润最大？并求出最大利润．
相关试题
=20，前n项和为Sn，且
，
的最小正周期为
的递增区间
ABC中，角A,B,C的对边分别为a,b,c,已知
求
的大小
的前
项和为
，求数列
的前
推荐套卷
某产品按质量分为10个档次，生产第一档（即最低档次）的利润是每件8元，每提高一个档次，利润每件增加2元，但每提高一个档次，在相同的时间内，产量减少3件。如果在规定的时间内，最低档次的产品可生产60件。
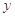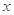（1）请写出相同时间内产品的总利润与档次之间的函数关系式，并写出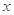的定义域．
（2）在同样的时间内，生产哪一档次产品的总利润最大？并求出最大利润．
粤公网安备 44130202000953号