(年云南省昆明市)如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15cm,CD=20cm,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)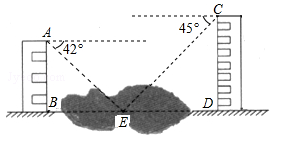
相关知识点
推荐套卷
(年云南省昆明市)如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15cm,CD=20cm,AB和CD之间有一景观池,小南在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°(点B、E、D在同一直线上),求两幢建筑物之间的距离BD(结果精确到0.1m).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)