(本小题12分)已知二次函数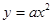 的图象经过点(2,1)。
的图象经过点(2,1)。
(1)求二次函数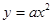 的解析式;
的解析式;
(2)一次函数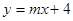 的图象与二次函数
的图象与二次函数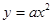 的图象交于点A(
的图象交于点A(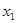 ,
,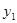 ),B(
),B(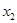 ,
,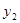 )两点
)两点
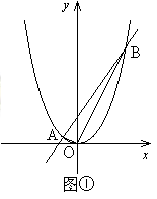
①当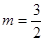 时(图①),求证:△AOB为直角三角形;
时(图①),求证:△AOB为直角三角形;
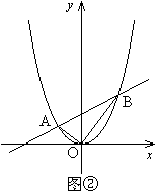
②试判断当 时(图②),△AOB的形状,并证明;
时(图②),△AOB的形状,并证明;
(3)根据第(2)问,说出一条你能得到的结论(不要求证明)。
(本小题12分)已知二次函数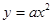 的图象经过点(2,1)。
的图象经过点(2,1)。
(1)求二次函数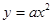 的解析式;
的解析式;
(2)一次函数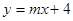 的图象与二次函数
的图象与二次函数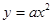 的图象交于点A(
的图象交于点A(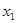 ,
,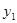 ),B(
),B(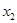 ,
,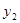 )两点
)两点
①当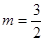 时(图①),求证:△AOB为直角三角形;
时(图①),求证:△AOB为直角三角形;
②试判断当 时(图②),△AOB的形状,并证明;
时(图②),△AOB的形状,并证明;
(3)根据第(2)问,说出一条你能得到的结论(不要求证明)。

