(崇左)如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.
(1)则点A、B、C的坐标分别是A(__,__),B(__,__),C(__,__);
(2)设经过A、B两点的抛物线解析式为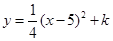 ,它的顶点为F,求证:直线FA与⊙M相切;
,它的顶点为F,求证:直线FA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.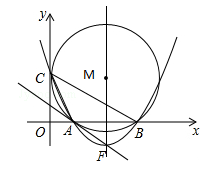
(崇左)如图,在平面直角坐标系中,点M的坐标是(5,4),⊙M与y轴相切于点C,与x轴相交于A、B两点.
(1)则点A、B、C的坐标分别是A(__,__),B(__,__),C(__,__);
(2)设经过A、B两点的抛物线解析式为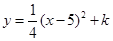 ,它的顶点为F,求证:直线FA与⊙M相切;
,它的顶点为F,求证:直线FA与⊙M相切;
(3)在抛物线的对称轴上,是否存在点P,且点P在x轴的上方,使△PBC是等腰三角形.如果存在,请求出点P的坐标;如果不存在,请说明理由.