(贺州)根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.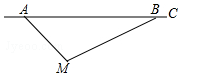
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据: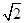 ≈1.41,
≈1.41,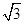 ≈1.73,
≈1.73, ≈2.24)
≈2.24)
(贺州)根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为 米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
(1)求测速点M到该公路的距离;
(2)通过计算判断此车是否超速.(参考数据: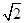 ≈1.41,
≈1.41,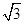 ≈1.73,
≈1.73, ≈2.24)
≈2.24)