已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.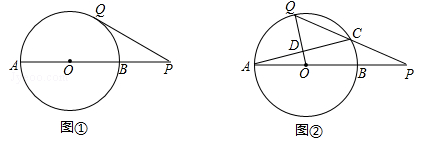
已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.