已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.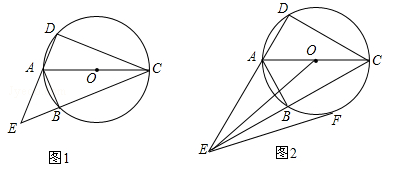
已知四边形ABCD内接于⊙O,∠ADC=90°,∠DCB<90°,对角线AC平分∠DCB ,延长DA,CB相交于点E.
(1)如图1,EB=AD,求证:△ABE是等腰直角三角形;
(2)如图2,连接OE,过点E作直线EF,使得∠OEF=30°,当∠ACE≥30°时,判断直线EF与⊙O的位置关系,并说明理由.