(广安)如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l: 经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线
经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线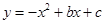 顶点E在直线l上.
顶点E在直线l上.
(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;
(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;
(3)设抛物线与y轴交于G点,当抛物线顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.
(广安)如图,边长为1的正方形ABCD一边AD在x负半轴上,直线l: 经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线
经过点B(x,1)与x轴,y轴分别交于点H,F,抛物线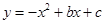 顶点E在直线l上.
顶点E在直线l上.
(1)求A,D两点的坐标及抛物线经过A,D两点时的解析式;
(2)当抛物线的顶点E(m,n)在直线l上运动时,连接EA,ED,试求△EAD的面积S与m之间的函数解析式,并写出m的取值范围;
(3)设抛物线与y轴交于G点,当抛物线顶点E在直线l上运动时,以A,C,E,G为顶点的四边形能否成为平行四边形?若能,求出E点坐标;若不能,请说明理由.