（成都）（本小题满分10分）如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC，BC及AB的延长线相交于点D，E，F，且BF=BC．⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G，交于点H，连接BD、FH．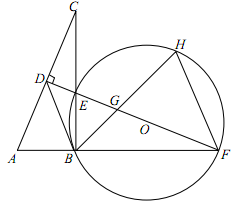
（1）求证：△ABC≌△EBF；
（2）试判断BD与⊙O的位置关系，并说明理由；
（3）若AB=1，求HG•HB的值．
相关试题
如图，已知O是坐标原点，B、C两点的坐标分别为(3，–1)、(2，1) ．
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)，画出图形；
(2)分别写出B、C两点的对应点B′、C′的坐标；
清明节期间，某中学团委组织八年级部分学生去离校2.4千米的某烈士陵园扫墓，回来时乘公交车所花时间比去时步行少用了36分钟，已知公交车速度是学生步行速度的5倍，求学生的步行速度．
有一道题“先化简，再求值：
．其中a =-5”马小虎同学做题时把“a = -5”错抄成了“a =5”，但他的计算结果却与别的同学一致，也是正确的，请你解释这是怎么回事?
；
，求
的度数.
粤公网安备 44130202000953号