（乐山）如图1，四边形ABCD中，∠B=∠D=90°，AB=3，BC=2，tanA=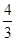
.
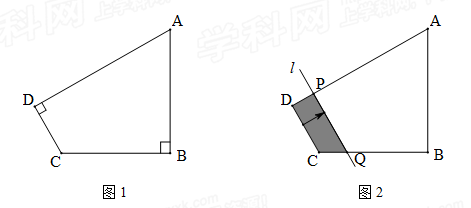
（1）求CD边的长；
（2）如图2，将直线CD边沿箭头方向平移，交DA于点P,交CB于点Q （点Q运动到点B停止），设DP=x，四边形PQCD的面积为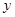
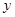，求与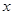
的函数关系式，并求出自变量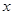的取值范围.
相关试题
（乐山）如图1，四边形ABCD中，∠B=∠D=90°，AB=3，BC=2，tanA=.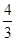
（1）求CD边的长；
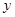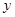（2）如图2，将直线CD边沿箭头方向平移，交DA于点P,交CB于点Q （点Q运动到点B停止），设DP=x，四边形PQCD的面积为，求与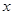的函数关系式，并求出自变量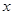的取值范围.
．
，4．
．
．
AB，则点C表示的数是；
BD，求线段AD的长（用含m，n的式子表示）．
粤公网安备 44130202000953号