如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=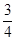 x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.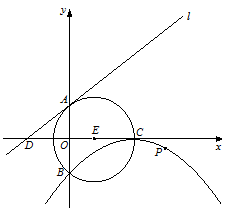
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.
如图,⊙E的圆心E(3,0),半径为5,⊙E与y轴相交于A、B两点(点A在点B的上方),与x轴的正半轴相交于点C;直线l的解析式为y=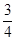 x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
x+4,与x轴相交于点D;以C为顶点的抛物线经过点B.
(1)求抛物线的解析式;
(2)判断直线l与⊙E的位置关系,并说明理由;
(3) 动点P在抛物线上,当点P到直线l的距离最小时,求出点P的坐标及最小距离.