（·辽宁葫芦岛）在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．
（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；
（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，
（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．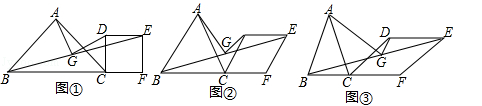
（·辽宁葫芦岛）在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．
（1）如图①，当∠BAC=∠DCF=90°时，直接写出AG与DG的位置和数量关系；
（2）如图②，当∠BAC=∠DCF=60°时，试探究AG与DG的位置和数量关系，
（3）当∠BAC=∠DCF=α时，直接写出AG与DG的数量关系．
,……
=;
的值.
为实数，
，求
.
粤公网安备 44130202000953号