（·辽宁沈阳）如图，已知一次函数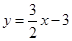
与反比例函数
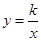的图象相交于点A（4，n），与x轴相交于点B．
（1）填空：n的值为 ，k的值为 ；
（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；
（3）考察反比函数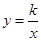的图象，当
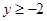时，请直接写出自变量x的取值范围．
相关试题
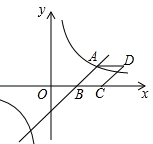
（·辽宁沈阳）如图，已知一次函数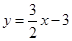与反比例函数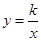的图象相交于点A（4，n），与x轴相交于点B．
（1）填空：n的值为 ，k的值为 ；
（2）以AB为边作菱形ABCD，使点C在x轴正半轴上，点D在第一象限，求点D的坐标；
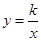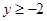（3）考察反比函数的图象，当时，请直接写出自变量x的取值范围．
=0
-
+(
)2
.
，那么关于x，y的二元一次方程组
粤公网安备 44130202000953号