（1）在下列横线上用含有a，b的代数式表示相应图形的面积．①

更新 2022-09-03
科目数学
题型解答题
难度中等
浏览 1352

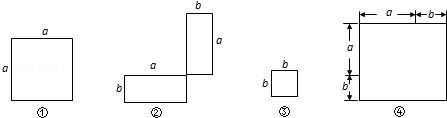
（1）在下列横线上用含有a，b的代数式表示相应图形的面积．
① ② ③ ④
（2）通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表示：；
（3）利用（2）的结论计算997²+6×997+9的值．

相关试题

近年来，我市大力发展城市快速交通，小王开车从家到单位有两条路线可选择，路线 $A$ 为全程 $25 km$ 的普通道路，路线 $B$ 包含快速通道，全程 $30 km$ ，走路线 $B$ 比走路线 $A$ 平均速度提高 $50 %$ ，时间节省 $6 \min$ ，求走路线 $B$ 的平均速度．

题型：未知
难度：未知

收藏答案/解析

一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

（1）该学习小组发现，摸到白球的频率在一个常数附近摆动，这个常数是　　．（精确到 $0.01)$ ，由此估出红球有　　个．

（2）现从该袋中摸出2个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到1个白球，1个红球的概率．

题型：未知
难度：未知

收藏答案/解析

2020年6月1日起，公安部在全国开展"一盔一带"安全守护行动．某校小交警社团在交警带领下，从5月29日起连续6天，在同一时段对某地区一路口的摩托车和电动自行车骑乘人员佩戴头盔情况进行了调查，并将数据绘制成如下图表：

2020年6月2日骑乘人员头盔佩戴情况统计表

	骑乘摩托车	骑乘电动自行车
戴头盔人数	18	72
不戴头盔人数	2	$m$

（1）根据以上信息，小明认为6月3日该地区全天摩托车骑乘人员头盔佩戴率约为 $95 %$ ．你是否同意他的观点？请说明理由；

（2）相比较而言，你认为需要对哪类人员加大宣传引导力度？为什么？

（3）求统计表中 $m$ 的值．

题型：未知
难度：未知

收藏答案/解析

（1）计算： ${(- π)}^{0} + {(\frac{1}{2})}^{- 1} - \sqrt{3} \sin 60 °$ ；

（2）解不等式组： $\{\begin{matrix} 3 x - 1 ⩾ x + 1, \\ x + 4 < 4 x - 2 \cdot \end{matrix}$

题型：未知
难度：未知

收藏答案/解析

如图，已知 $∠ MON = 90 °$ ， $OT$ 是 $∠ MON$ 的平分线， $A$ 是射线 $OM$ 上一点， $OA = 8 cm$ ．动点 $P$ 从点 $A$ 出发，以 $1 cm / s$ 的速度沿 $AO$ 水平向左作匀速运动，与此同时，动点 $Q$ 从点 $O$ 出发，也以 $1 cm / s$ 的速度沿 $ON$ 竖直向上作匀速运动．连接 $PQ$ ，交 $OT$ 于点 $B$ ．经过 $O$ 、 $P$ 、 $Q$ 三点作圆，交 $OT$ 于点 $C$ ，连接 $PC$ 、 $QC$ ．设运动时间为 $t (s)$ ，其中 $0 < t < 8$ ．

（1）求 $OP + OQ$ 的值；

（2）是否存在实数 $t$ ，使得线段 $OB$ 的长度最大？若存在，求出 $t$ 的值；若不存在，说明理由．

（3）求四边形 $OPCQ$ 的面积．

题型：未知
难度：未知

收藏答案/解析

推荐套卷

热门套卷