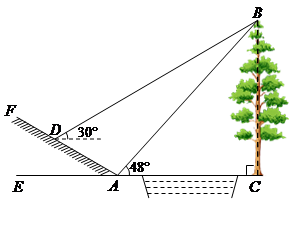（.河南省，第20题，9分）如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30º，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，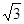
≈1.73）
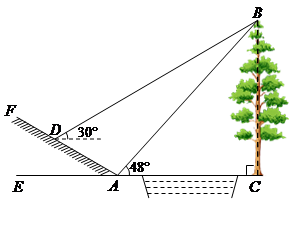
（.河南省，第20题，9分）如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30º，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11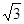，≈1.73）
粤公网安备 44130202000953号