（本小题满分12分）如图，已知底角为450角的等腰梯形ABCD，底边BC长为7cm，腰长为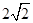
cm，当一条垂直于底边BC（垂足为F）的直线
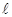把梯形ABCD分成两部分，令|BF|x
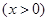，求左边部分的面积y关于x的函数解析式，并画出图象。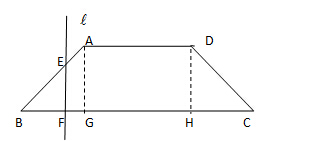
相关试题
在R上单调递减；q：不等式
＞1的解集为R，如果“p或q”为真，且“p且q”为假，求c的取值范围。
,且
,⑴求
的取值范围;⑵求证
;⑶求函数
的取值范围.
,满足f(
)
=f(0),⑴求函数f(x)的最小正周期;⑵求函数f(x)在
上的最大值和最小值.
,最小值为
,求a,b 的
值.推荐套卷
（本小题满分12分）如图，已知底角为450角的等腰梯形ABCD，底边BC长为7cm，腰长为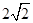cm，当一条垂直于底边BC（垂足为F）的直线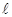把梯形ABCD分成两部分，令|BF|x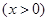，求左边部分的面积y关于x的函数解析式，并画出图象。
粤公网安备 44130202000953号