在正方体ABCD－A1B1C1D1中，E是CD的中点，连接AE并延长与BC的延长线交于点F，连接BE并延长交AD的延长线于点G，连接FG．
求证：直线FG⊂平面ABCD且直线FG∥直线A1B1．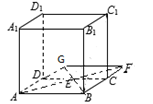
相关试题
的最大值与最小值．
，1)，点B在y轴上，直线AB的倾斜角为
，求点B的坐标．相关知识点
推荐套卷
在正方体ABCD－A1B1C1D1中，E是CD的中点，连接AE并延长与BC的延长线交于点F，连接BE并延长交AD的延长线于点G，连接FG．
求证：直线FG⊂平面ABCD且直线FG∥直线A1B1．
粤公网安备 44130202000953号