某公司推销一种产品，公司付给推销员的月报酬有两种方案如图所示：其中方案一所示图形是顶点B在原点的抛物线的一部分，方案二所示图形是射线．设推销员推销产品的数量为x（件），付给推销员的月报酬为y（元）．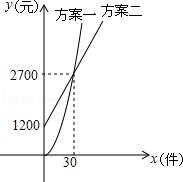
（1）分别求两种方案中y关于x的函数关系式；
（2）当销售达到多少件时，两种方案月报酬差额将达到3800元？
（3）若公司决定改进“方案二”：保持基本工资不变，每件报酬增加m元，使得当销售员销售产量达到40件时，两种方案的报酬差额不超过1000元．求m的取值范围．
相关试题
，求弦MN的长．如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC边上的中线BD反向延长线交y轴负半
轴于E，双曲线
(x＞0)的图像经过点A，若S△BEC=10，则k等于 .
=
，
=
，
=
。问：
时。现在，甲和乙都最多只能工作60小时，丙最多只能工作35小时，三队工作时间之和为100小时完成工程，则甲最多工作多少小时？相关知识点
推荐套卷
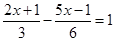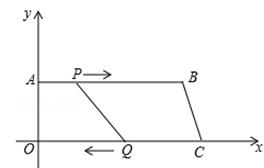
粤公网安备 44130202000953号