如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，点A，B，C的坐标分别为（0，﹣1），（1，﹣1），（5，﹣1）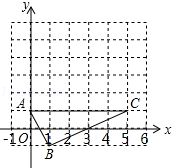
（1）判断△ABC的形状；
（2）将△ABC绕点C顺时针旋转90°得到△A1B1C，请在网格中画出△A1B1C，并直接写出点A1和B1的坐标；
（3）将△ABC绕线段AC所在直线旋转一周，求所得几何体的表面积．
；
；
；
πR3，求半径为3.5cm的球的体积．（π取3.14，结果保留五个有效数字）相关知识点
推荐套卷
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，点A，B，C的坐标分别为（0，﹣1），（1，﹣1），（5，﹣1）
（1）判断△ABC的形状；
（2）将△ABC绕点C顺时针旋转90°得到△A1B1C，请在网格中画出△A1B1C，并直接写出点A1和B1的坐标；
（3）将△ABC绕线段AC所在直线旋转一周，求所得几何体的表面积．
粤公网安备 44130202000953号