(本小题满分13分)
已知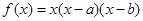 ,点A(s, f(s)), B(t, f(t))
,点A(s, f(s)), B(t, f(t))
(Ⅰ)若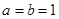 ,求函数
,求函数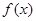 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数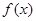 的导函数
的导函数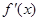 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|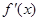 |≤
|≤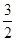 恒成立,求函数
恒成立,求函数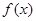 的解析表达式;
的解析表达式;
(Ⅲ)若0<a<b, 函数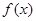 在
在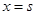 和
和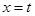 处取得极值,且
处取得极值,且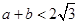 ,证明:
,证明: 与
与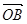 不可能垂直.
不可能垂直.
推荐套卷
(本小题满分13分)
已知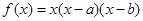 ,点A(s, f(s)), B(t, f(t))
,点A(s, f(s)), B(t, f(t))
(Ⅰ)若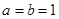 ,求函数
,求函数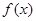 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数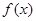 的导函数
的导函数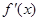 满足:当|x|≤1时,有|
满足:当|x|≤1时,有|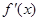 |≤
|≤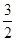 恒成立,求函数
恒成立,求函数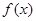 的解析表达式;
的解析表达式;
(Ⅲ)若0<a<b, 函数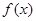 在
在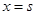 和
和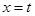 处取得极值,且
处取得极值,且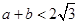 ,证明:
,证明: 与
与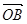 不可能垂直.
不可能垂直.