如图△ABC内接于⊙O，且AB=AC，过点A的直线交⊙O于点P，交BC的延长线于点D．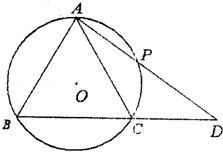
（Ⅰ）求证：AC2=AP•AD；
（Ⅱ）若∠ABC=60°，⊙O的半径为1，且P为弧AC的中点，求AD的长．
是
的两倍，
是
倍，试求这组数据的相关系数
．（精确到
）
，需要研究它和原料有效成分含量
之间的相关关系，现取
对观测值，计算得
，求
）
为坐标原点, 
为直线
上动点, 
, 
, 求
点的轨迹方程.
，
且
，
，求
的值．
，
，求
的范围．相关知识点
推荐套卷
如图△ABC内接于⊙O，且AB=AC，过点A的直线交⊙O于点P，交BC的延长线于点D．
（Ⅰ）求证：AC2=AP•AD；
（Ⅱ）若∠ABC=60°，⊙O的半径为1，且P为弧AC的中点，求AD的长．
粤公网安备 44130202000953号