在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.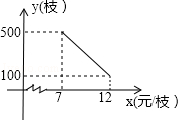
(1)试求y与x之间的函数关系式;
(2)若“康乃馨”的进价为5元/枝,且要求每枝的销售盈利不少于1元,问:在此次活动中,他们最多可购进多少数量的康乃馨?
相关知识点
推荐套卷
在“母亲节”期间,某校部分团员准备购进一批“康乃馨”进行销售,并将所得利润捐给贫困同学的母亲.根据市场调查,这种“康乃馨”的销售量y(枝)与销售单价x(元/枝)之间成一次函数关系,它的部分图象如图.
(1)试求y与x之间的函数关系式;
(2)若“康乃馨”的进价为5元/枝,且要求每枝的销售盈利不少于1元,问:在此次活动中,他们最多可购进多少数量的康乃馨?