(本小题满分12分)设定义在区间 上的函数
上的函数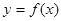 的图像为C,点A、B的坐标分别为
的图像为C,点A、B的坐标分别为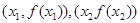 且
且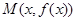 为图像C上的任意一点,O为坐标原点,当实数
为图像C上的任意一点,O为坐标原点,当实数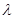 满足
满足 时,记向量
时,记向量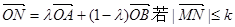 恒成立,则称函数
恒成立,则称函数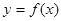 在区间
在区间 上可在标准
上可在标准 下线性近似,其中
下线性近似,其中 是一个确定的正数。
是一个确定的正数。
(Ⅰ)求证:A、B、N三点共线
(Ⅱ)设函数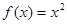 在区间
在区间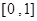 上可在标准
上可在标准 下线性近似,求
下线性近似,求 的取值范围;
的取值范围;
(Ⅲ)求证:函数 在区间
在区间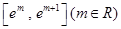 上可在标准
上可在标准 下线性近似。
下线性近似。
(参考数据: 2.718,
2.718, 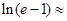 0.541)
0.541)
推荐套卷
(本小题满分12分)设定义在区间 上的函数
上的函数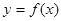 的图像为C,点A、B的坐标分别为
的图像为C,点A、B的坐标分别为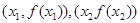 且
且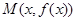 为图像C上的任意一点,O为坐标原点,当实数
为图像C上的任意一点,O为坐标原点,当实数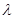 满足
满足 时,记向量
时,记向量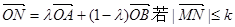 恒成立,则称函数
恒成立,则称函数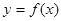 在区间
在区间 上可在标准
上可在标准 下线性近似,其中
下线性近似,其中 是一个确定的正数。
是一个确定的正数。
(Ⅰ)求证:A、B、N三点共线
(Ⅱ)设函数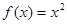 在区间
在区间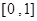 上可在标准
上可在标准 下线性近似,求
下线性近似,求 的取值范围;
的取值范围;
(Ⅲ)求证:函数 在区间
在区间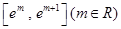 上可在标准
上可在标准 下线性近似。
下线性近似。
(参考数据: 2.718,
2.718, 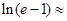 0.541)
0.541)