如图，已知直线y=2x分别与双曲线y=
，y=
（x＞0）交于P、Q两点，且OP=2OQ，点A是双曲线y=上的动点，过A作AB∥x轴，AC∥y轴，分别交双曲线y=（x＞0）于点B、C．连接BC．
（1）求k的值；
（2）随着点A的运动，△ABC的面积是否发生变化？若不变，求出△ABC的面积，若改变，请说明理由．
（3）直线y=2x上是否存在点D，使得点A、B、C、D为顶点的四边平行四边形？若能，求出相应点A的坐标；若不能，请说明理由．
相关试题
（本题10分）已知：如图，在△ABC中，AB＝AC，点D是边BC的中点，以BD为直径作圆O，交边AB于点P，连接PC，交AD于点E．
（1）求证：AD是圆O的切线：
（2）若PC是圆O的切线，BC＝8，求DE的长．
（本题10分）如图，正方形网格中每个小正方形边长都是1，每个小格的顶点叫格点，以格点为顶点的三角形叫做格点三角形．
（1）格点△ABC的面积为；
（2）画出格点△ABC绕点C逆时针旋转90°后的△A1B1C1，并求出在旋转过程中，点B所经过的路径长．
（本题10分）如图，已知AD是△ABC的高，AE是△ABC的外接圆的直径．
（1）求证AC·AB＝AD·AE；
（2）若AB＝8，AC＝5，AD＝4，求⊙O的面积．
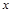的方程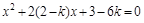
，
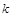的值及方程的另一根；相关知识点
推荐套卷
粤公网安备 44130202000953号