有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.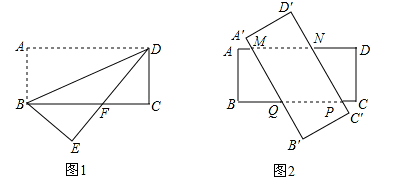
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),试判断四边形MNPQ的形状,并证明.
推荐套卷
有两张相同的矩形纸片ABCD和A′B′C′D′,其中AB=3,BC=8.
(1)若将其中一张矩形纸片ABCD沿着BD折叠,点A落在点E处(如图1),设DE与BC相交于点F,求BF的长;
(2)若将这两张矩形纸片交叉叠放(如图2),试判断四边形MNPQ的形状,并证明.