如图，甲、乙两个企业的用电负荷量
关于投产持续时间
（单位：小时）的关系
均近似地满足函数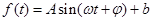
．
（1）根据图象，求函数
的解析式；
（2）为使任意时刻两企业用电负荷量之和不超过
，现采用错峰用电的方式，让企业乙比企业甲推迟
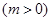小时投产，求的最小值．
相关试题
，求
。
的定义域为
，求下列函数的定义域：
；（2）y＝
。
且
。
的值；
和g[
的解析式。推荐套卷
如图，甲、乙两个企业的用电负荷量关于投产持续时间（单位：小时）的关系均近似地满足函数．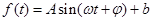
（1）根据图象，求函数的解析式；
（2）为使任意时刻两企业用电负荷量之和不超过，现采用错峰用电的方式，让企业乙比企业甲推迟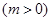小时投产，求的最小值．
粤公网安备 44130202000953号