设A是圆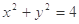 上的任意一点,
上的任意一点,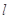 是过点A与
是过点A与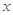 轴垂直的直线,D是直线
轴垂直的直线,D是直线 与
与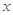 轴的交点,点M在直线
轴的交点,点M在直线 上,且满足
上,且满足 .当点A在圆上运动时,记点M的轨迹为曲线
.当点A在圆上运动时,记点M的轨迹为曲线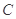 .
.
(1)求曲线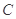 的标准方程;
的标准方程;
(2)设曲线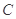 的左右焦点分别为
的左右焦点分别为 、
、 ,经过
,经过 的直线
的直线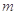 与曲线
与曲线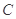 交于P、Q两点,若
交于P、Q两点,若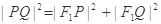 ,求直线
,求直线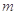 的方程.
的方程.
相关知识点
推荐套卷
设A是圆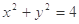 上的任意一点,
上的任意一点,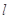 是过点A与
是过点A与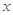 轴垂直的直线,D是直线
轴垂直的直线,D是直线 与
与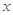 轴的交点,点M在直线
轴的交点,点M在直线 上,且满足
上,且满足 .当点A在圆上运动时,记点M的轨迹为曲线
.当点A在圆上运动时,记点M的轨迹为曲线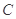 .
.
(1)求曲线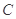 的标准方程;
的标准方程;
(2)设曲线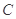 的左右焦点分别为
的左右焦点分别为 、
、 ,经过
,经过 的直线
的直线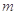 与曲线
与曲线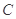 交于P、Q两点,若
交于P、Q两点,若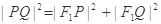 ,求直线
,求直线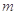 的方程.
的方程.