(1).已知抛物线的焦点是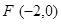
,求它的标准方程 ;
(2).已知椭圆的长轴长是短轴长的3倍,且经过点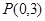
，求椭圆的标准方程;
(3).已知双曲线两个焦点分别为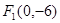
,
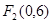,双曲线上一点
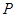到
,
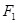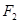的距离差的绝对值等于8, 求双曲线的方程.
相关试题
，公差
不为零，
，且
成等比数列;
满足
，求数列
项和
.
中，角
所对的边分别为
，已知
，
，
．
的值；
的值．
，若方程
在
上有且仅一个实根，求实数
的取值范围；
时，求函数
在
上的最大值.
，其中常数
满足
，判断函数
的单调性；
，求
时的
的取值范围.相关知识点
推荐套卷
(1).已知抛物线的焦点是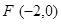,求它的标准方程 ;
(2).已知椭圆的长轴长是短轴长的3倍,且经过点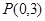，求椭圆的标准方程;
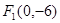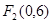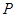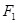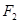(3).已知双曲线两个焦点分别为,,双曲线上一点到,的距离差的绝对值等于8, 求双曲线的方程.
粤公网安备 44130202000953号