（本题12分）如图，A、B、C、D都在同一个与水平面垂直的平面内，B、D为两岛上的两座灯塔的塔顶，测量船于水面A处测得B点和D点的仰角分别为75°、30°，于水面C处测得B点和D点的仰角均为60°，AC＝0．1km．试探究图中B、D间距离与另外哪两点间距离相等，然后求B、D的距离（计算结果精确到0．01km，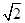
≈1．414，
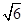≈2．449）．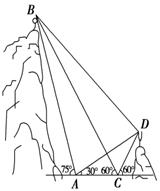
的解集为C (Ⅰ)求集合C； (Ⅱ)若方程
在C上有解，求实数a的取值范围； (Ⅲ)记f(x)在C上的值域为A，若
的值域为B，且
，求非正实数t的取值范围。
sinx)－1,x∈R(1)求f (x)的最小正周期T；(2)求f (x)的单调递增区间.相关知识点
推荐套卷
（本题12分）如图，A、B、C、D都在同一个与水平面垂直的平面内，B、D为两岛上的两座灯塔的塔顶，测量船于水面A处测得B点和D点的仰角分别为75°、30°，于水面C处测得B点和D点的仰角均为60°，AC＝0．1km．试探究图中B、D间距离与另外哪两点间距离相等，然后求B、D的距离（计算结果精确到0．01km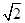，≈1．414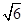，≈2．449）．
粤公网安备 44130202000953号