在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖. 已知教师甲投进每个球的概率都是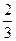
．
（Ⅰ）记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望；
（Ⅱ）求教师甲在一场比赛中获奖的概率；
（Ⅲ）已知教师乙在某场比赛中，6个球中恰好投进了4个球，求教师乙在这场比赛中获奖的概率；教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗？
在区间
上的单调性并用定义证明；
，求
的取值范围.
．
的图象，并比较
大小.
，求证：
，B=
.
，求实数m的值；
，求实数m的取值范围.
．
的值域；(Ⅱ)设
，若对
， 
，恒
成立，试
求实数
的取值范围推荐套卷
在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖. 已知教师甲投进每个球的概率都是．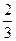
（Ⅰ）记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望；
（Ⅱ）求教师甲在一场比赛中获奖的概率；
（Ⅲ）已知教师乙在某场比赛中，6个球中恰好投进了4个球，求教师乙在这场比赛中获奖的概率；教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗？
粤公网安备 44130202000953号