(本小题满分14分)北京市周边某工厂生产甲、乙两种产品.一天中,生产一吨甲产品、一吨乙产品所需要的煤、水以及产值如表所示:
| |
用煤(吨) |
用水(吨) |
产值(万元) |
| 生产一吨甲种产品 |
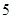 |
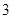 |
 |
| 生产一吨乙种产品 |
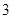 |
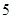 |
 |
在 会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多
会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多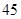 吨,用水最多
吨,用水最多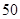 吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?
吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?
推荐套卷
(本小题满分14分)北京市周边某工厂生产甲、乙两种产品.一天中,生产一吨甲产品、一吨乙产品所需要的煤、水以及产值如表所示:
| |
用煤(吨) |
用水(吨) |
产值(万元) |
| 生产一吨甲种产品 |
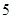 |
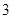 |
 |
| 生产一吨乙种产品 |
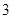 |
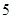 |
 |
在 会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多
会议期间,为了减少空气污染和废水排放.北京市对该厂每天用煤和用水有所限制,每天用煤最多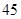 吨,用水最多
吨,用水最多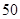 吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?
吨.问该厂如何安排生产,才能是日产值最大?最大的产值是多少?