如图,下列几何体是由棱长为1的小立方体按一定规律在地面上摆成的,现将露出的表面都涂上颜色(下底面不涂色),则所给几何体中只有两个面涂色的小立方体的个数分别为:
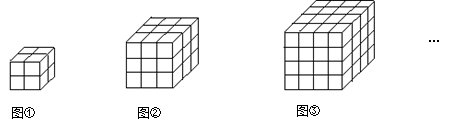
第1个几何体:最下面一层个数=4;
第2个几何体:最下面一层个数+中间一层个数+最上面一层个数=4+4+4=12;
第3个几何体:最下面一层个数+中间两层个数+最上面一层个数=4+8+8=20;
……
总结规律,回答下列问题:
(1)第4个几何体中只有两个面涂色的小立方体共有 ▲个;
(2)第n个几何体中只有两个面涂色的小立方体共有多少个?(用含字母n的式子表示.)