已知：如图，点A（3，4）在直线y=kx上，过A作AB⊥x轴于点B．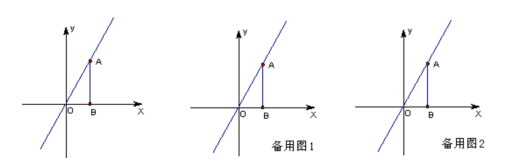
（1）求k的值；
（2）设点B关于直线y=kx的对称点为C点，求ΔABC外接圆的面积；
（3）抛物线y=
－1与x轴的交点为Q，试问在直线y=kx上是否存在点P，使得
∠CPQ=∠OAB，如果存在，请求出P点的坐标；如果不存在，请说明理由．
．
时，写出
的单调区间；
时，求
的方程
的解的个数．
的不等式：
．
是定义在
上的增函数．
，试比较
的大小，并说明理由；
，不等式
恒成立，求实数
的取值范围．
的定义域为集合A，函数
的定义域为集合B．
，求实数
的取值范围．
．
的值；
的值域．推荐套卷
已知：如图，点A（3，4）在直线y=kx上，过A作AB⊥x轴于点B．
（1）求k的值；
（2）设点B关于直线y=kx的对称点为C点，求ΔABC外接圆的面积；
（3）抛物线y=－1与x轴的交点为Q，试问在直线y=kx上是否存在点P，使得
∠CPQ=∠OAB，如果存在，请求出P点的坐标；如果不存在，请说明理由．
粤公网安备 44130202000953号