某中学需在短跑、跳远、乒乓球、跳高四类体育项目中各选一名同学参加中学生运动会，根据平时成绩，把各项目进入复选的人员情况绘制成不完整的统计图、表如下：复选人员扇形统计图：复选人员统计表：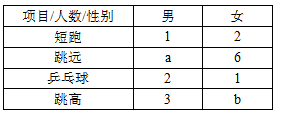
（1）求a、b的值；
（2）求扇形统计图中跳远项目对应圆心角的度数；
（3）用列表法或画树状图的方法求在短跑和乒乓球项目中选出的两位同学都为男生的概率．
相关试题
的边
在
的边
上，顶点
、
分别在边
、
上，
，垂足为
．已知
，
.
为正方形时，求该正方形的边长；
面积为18时，求矩形的长和宽．
中，
，
，
，求（1）
的值. 
中，
、
、
分别是
、AC、BC上的点，联结
、EF交于点G，且
.
相似的三角形（不用证明）；
，试求
的值．
. 求证：(1)
；(2) 
．
在平行四边形
的边
的延长线上，连结
交
于点
．求证：
.
相关知识点
推荐套卷
某中学需在短跑、跳远、乒乓球、跳高四类体育项目中各选一名同学参加中学生运动会，根据平时成绩，把各项目进入复选的人员情况绘制成不完整的统计图、表如下：复选人员扇形统计图：复选人员统计表：
（1）求a、b的值；
（2）求扇形统计图中跳远项目对应圆心角的度数；
（3）用列表法或画树状图的方法求在短跑和乒乓球项目中选出的两位同学都为男生的概率．
粤公网安备 44130202000953号