如图，沿AC方向开山修一条公路，为了加快施工进度，要在小山的另一边寻找点E同时施工，从AC上的一点B取∠ABD=127º，沿BD的方向前进，取∠BDE=37º，测得BD=520m，并且AC、BD和DE在同一平面内.
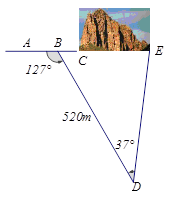
（1）施工点E 离D多远正好能使A、C、E成一直线（结果保留整数）
（2）在（1）的条件下，若BC=80m，求公路CE段的长（结果保留整数）
（参考数据：sin37º≈0.60, cos37º≈ 0.80, tan37º≈0.75)）
相关试题
如图，已知直线
交⊙O于A、B两点，AE是⊙O的直径,点C为⊙O上一点，且AC平分∠PAE，过C作
，垂足为D.(1) 求证：CD为⊙O的切线；
(2) 若CD=2AD，⊙O的直径为10，求线段AC的长.
如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m．若矩形的面积为4m2，请你计算AB的长度（可利用的围墙长度超过6m）．
为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1.6米，标杆为3.1米，且BC=1米，CD=5米，请你根据所给出的数据求树高ED.
已知二次函数y=x2+bx+c中，函数y与自变量x的部分对应值如下表：
| x |
… |
-1 |
0 |
1 |
2 |
3 |
4 |
… |
| y |
… |
8 |
3 |
0 |
-1 |
0 |
3 |
… |
(1) 求该二次函数的解析式；
(2) 当x为何值时，y有最小值，最小值是多少？
(3)
若A（m,y1）,B(m+2, y2)两点都在该函数的图象上，计算当m取何值时，
三个顶点的坐标分别为
顺时针旋转
后得到的
，并求出
的长.
相关知识点
推荐套卷
粤公网安备 44130202000953号