【2015江苏高考,18】(本小题满分16分)如图,在平面直角坐标系xOy中,已知椭圆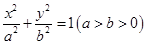 的离心率为
的离心率为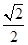 ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.
推荐套卷
【2015江苏高考,18】(本小题满分16分)如图,在平面直角坐标系xOy中,已知椭圆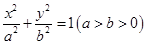 的离心率为
的离心率为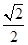 ,且右焦点F到左准线l的距离为3.
,且右焦点F到左准线l的距离为3.
(1)求椭圆的标准方程;
(2)过F的直线与椭圆交于A,B两点,线段AB的垂直平分线分别交直线l和AB于点P,C,若PC=2AB,求直线AB的方程.