(本题12分)如图,直线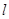 :
: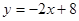 分别与
分别与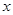 轴、
轴、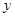 轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE;
轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE;
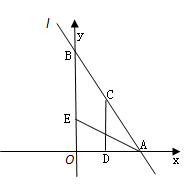
(1)填空:点C的坐标为( , );点E的坐标为( , );
(2)直线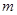 过点E,且将△AOB分成面积比为1:2的两部分,求直线
过点E,且将△AOB分成面积比为1:2的两部分,求直线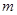 的表达式;
的表达式;
(3)点P在x轴上运动,
①当PC+PE取最小值时,求点P的坐标及PC+PE的最小值;
②当PC-PE取最大值时,求点P的坐标及PC-PE的最大值;
(本题12分)如图,直线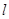 :
: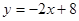 分别与
分别与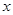 轴、
轴、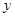 轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE;
轴交于A、B两点,点C线段AB上,作CD⊥x轴于D, CD="2OD," 点E线段OB上,且AE=BE;

(1)填空:点C的坐标为( , );点E的坐标为( , );
(2)直线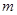 过点E,且将△AOB分成面积比为1:2的两部分,求直线
过点E,且将△AOB分成面积比为1:2的两部分,求直线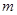 的表达式;
的表达式;
(3)点P在x轴上运动,
①当PC+PE取最小值时,求点P的坐标及PC+PE的最小值;
②当PC-PE取最大值时,求点P的坐标及PC-PE的最大值;