（本题9分）某中学开展“感恩父母”演讲比赛活动，八（1）、八（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示。
（1）根据下图，分别求出两班复赛的平均成绩和方差；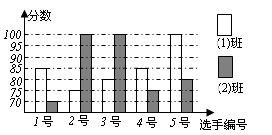
（2）根据（1）的计算结果，哪个班级的复赛成绩较好？为什么？
相关试题
（本题9分）某中学开展“感恩父母”演讲比赛活动，八（1）、八（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示。
（1）根据下图，分别求出两班复赛的平均成绩和方差；
（2）根据（1）的计算结果，哪个班级的复赛成绩较好？为什么？
下结论：
是等腰三角形，并说明理由。
∠1=∠3，∠C=110°，求∠2的度数。
粤公网安备 44130202000953号